探検 XMLボキャブラリの世界 第11回
第11回:数式のボキャブラリ ~MathML~
著者:岸 和孝(JAGAT客員研究員)
前回まで,一般の印刷において専門化された組版対象となっている「分子構造図(CML)」,「地図(GML)」,「楽譜(MusicXML)」のボキャブラリについて見てきましたので,今回は,同様に専門性の高い「数式」についても触れないわけにはいかないでしょう。数式のボキャブラリについては,すでに「MathMLによる数式表現」と題して本誌(Vol.39 No.6~No.10)で5回にわたって説明しましたが,それを連載したのは2年も前のことになります。今回は,最近の動向を含めて,そのバックナンバーの要約を述べることとします。
MathMLのボキャブラリ
一般のWebページで数式が現れることはほとんどありませんが,教育や製造業の分野では数式は必ず現れるでしょう。しかし,HTMLのボキャブラリーには数式を表すためのタグは用意されていませんので,数式に分数や平方根などの成分が含まれると,HTMLではまったく表しようがありません。そうした数式は,なんらかのツールでラスター図形かベクトル図形として描いてからGIF形式などの画像へ変換し,それをimgタグで参照することになります。そのため数式の変更が出る度にそうした作業が生じることになります。実に効率が悪い工程と言えます。
そこで,数式を表すためのボキャブラリとしてMathMLの勧告第1版が1998年に,MathMLの勧告第2版が2003年にそれぞれW3Cによって策定され,XHTMLと組み合わせた複合文書としてWebで利用できるようになりました。しかし,現状では複合文書が扱えるWebブラウザは,Mozilla(FireFox),amaya,xfyに限られているようです。Internet Explorerの最新バージョンの7でも複合文書は直接閲覧できず,MathMLを閲覧するにはMathPlayerというプラグインが必要です。
MathMLには,2種類のボキャブラリがあります。ひとつは,数式の表示を目的とした表示表記(presentation markup)のボキャブラリで,もうひとつは,数式の内容,すなわち意味を表すことを目的とした内容表記(content markup)のボキャブラリです。数式を扱う人々(数学者,技術者,教育関係者)が必要とする表記は内容表記です。ここが肝心なところです。内容表記から表示表記への変換は可能です。さらに,これらのボキャブラリは混ぜて使うこともできます。
XML(MathML)以前において,数式の表示を目的とした表記法には,よく知られたTeXがあります。また数式の内容(意味)を表すことを目的とした表記法には,EqnとezMathがあります。しかし,これらはTeXほどには普及していないようです。
MathMLにおける表示表記のボキャブラリは,TeXからの移行を意識して開発されています。つまり,TeXの膨大なレガシーデータを内容表記のボキャブラリへ書き換えるのでは手間と費用が余りに大きすぎますので,TeXからの変換が可能な表示表記のボキャブラリが開発されたわけです。実際にTeXからMathMLへ変換するツールが利用できます。これからの応用では,内容表記のボキャブラリが選ばれることが多くなるでしょう。
MathMLの例
ここで,具体的なMathMLの例を紹介します。例えば,学校で学ぶ2次方程式の解は,図1のように表されます。これを表示表記のボキャブラリで表すと図2のようになります。同様に,内容表記のボキャブラリで表すと図3のようになります。
▼図1 2次方程式の解
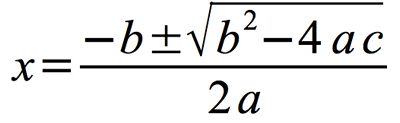
表示表記のボキャブラリでは,"mi"は変数を示す識別子,"mn"は数値,"mo"は演算子,"msup"は上付き,"⁢"は非表示の乗算記号,"mfrac"は分数,"±"は正負記号,"msqrt"は平方根,"mrow"はグループを,それぞれ意味します。
▼図2 2次方程式の解の表示表記
<math>
<mi>x</mi>
<mo>=</mo>
<mfrac>
<mrow>
<mo>-</mo><mi>b</mi><mo>±</mo>
<msqrt>
<mrow>
<msup><mi>b</mi><mn>2</mn></msup>
<mo>-</mo>
<mrow>
<mn>4</mn>
<mo>⁢</mo>
<mi>a</mi>
<mo>⁢</mo>
<mi>c</mi>
</mrow>
</mrow>
</msqrt>
</mrow>
<mrow>
<mn>2</mn><mo>⁢</mo><mi>a</mi>
</mrow>
</mfrac>
</math>
内容表記のボキャブラリでは,"apply"は数式への演算の適用,"eq"は等号,"divide"は除算,"root"は平方根,"minus"は減算,"power"は累乗,"times"は乗算をそれぞれ意味し,数式全体を演算可能な形で表します。例えば,「bの2乗」は,表示表記では「
▼図3 2次方程式の解の内容表記
<math>
<mrow>
<apply>
<eq/>
<ci>x</ci>
<apply>
<divide/>
<apply>
<mo>±</mo>
<apply>
<minus/><ci>b</ci>
</apply>
<apply>
<root/>
<apply>
<minus/>
<apply>
<power/><ci>b</ci><cn>2</cn>
</apply>
<apply>
<times/><cn>4</cn><ci>a</ci><ci>c</ci>
</apply>
</apply>
<cn>2</cn>
</apply>
</apply>
<apply>
<times/><cn>2</cn><ci>a</ci>
</apply>
</apply>
</apply>
</mrow>
</math>
数式は文章か画像か
ここで,数式は文章か画像かという問題について考えてみましょう。図4のような複雑な数式があるとします。これは「画像化された数式」です。では,その内容を文章で表すとどうなるでしょうか。数学教師はこう言うでしょう。「eのy乗の2乗の,yについてゼロからxまで積分し,そのxが無限大まで限りなく近づくときの極限値は,円周率の平方根を2で除した値と等しい」と。言うまでもなく,数式は数学で定めた「言語記号」で表されたものであり,数学では「画像化された数式」をそのまま扱うことが当たり前になっています。ちょうど楽譜の記号と同じ扱いです。
ところが,コンピュータの入力テキストは1次元ですから,こうした2次元の画像を表すには様々な特殊記号を使わなければなりません。例えば,図4の数式は,TeXでは「\mathop { \lim }\limits_{ x \to \infty } \int_0^x { \mathop e \nolimits^{ \mathop y\nolimits^2 } } dy = \frac{ { \sqrt \pi } } { 2 }」と表します。組版をするだけにしても,よほどTeXに慣れていないと表すことは困難でしょう。そこで数式を文章として表すことが考えられました。Eqnでは「lim( int from n to x ( e^y^2, y ), x=>inf ) = sqrt(pi) / 2」と表します。さらに進んだ形のezMathでは,「limit as x tends to infinity of integral from 0 to x wrt y of e^y^2 } = sqrt pi / 2」と表します。これらは英語ではありますが,文章として読めるものになっています。
ところで,OpenOfficeは,私が最近最も注目しているXMLツールのひとつです。OpenOfficeで数式を入力する時に利用できるエディターは,図4の数式を「lim csub { x rightarrow infinity } int from n to x { e ^ { y ^ 2 } } dy = sqrt{ π } over 2」と表現します。この表記から数式が描かれます。これは文章としての数式表現が重要であることを示していると言えます。なお,OpenOfficeの文書ファイルは,XMLデータをZIPで圧縮したもので,それを解凍すれば,MathMLで表した数式を得ることができます。
▼図4 複雑な数式
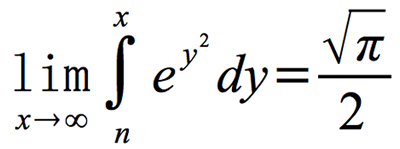
数式の表記とWebブラウザの関係
現在,MathMLによって表現されたWebコンテンツは普及していないようです。Internet Explorer(IE)がMathMLを含む複合文書を直接閲覧できないという状況が続いていることが最大の理由なのでしょうか。あるいは,TeX,Eqn,ezMathといったMathML以前の表記によって表現されたコンテンツがIEで閲覧可能[表1を参照]にも関わらず,それもまた普及していないこととも関係があるのでしょうか。私には何とも理解できない状況です。
▼表1 数式の表記とWebブラウザの関係
| 数式の表記 | HTMLでの表記 | 閲覧可能な Webブラウザ |
数式の画像化 |
|---|---|---|---|
| MathML | MathML | Mozilla | クライアント側で画像を生成 |
| MathML | MathML | IE | クライアント側でMathPlayerプラグインによって画像を生成 |
| TeX | imgタグのsrc属性 | IE,Mozilla | サーバー側でmimeTeXによって画像を生成 |
| Eqn | appletタグのeqnパラメータ | IE,Mozilla | サーバー側でEqnViewerによって画像を生成 |
| ezMath | embedタグのalt属性 | IE,Mozilla | クライアント側でezMathプラグインによって画像を生成 |
OpenMathとOMDoc
MathMLに関わる新しい規格があります。ひとつは,MathMLの内容表記を補完する内容辞書を定義するOpenMathです。もうひとつは,OpenMathによる文書形式を規定するOMDoc(Open Mathematical Documents)です。これらについては紙面の関係から今回は説明を割愛させていただきます。
PrintersCircle PrintersCircle 2007年5月号より転載
探検 XMLボキャブラリの世界
▲このページのTOPへ






